
項書き換えシステム(term rewriting system)は等式にもとづく柔軟な計算法 と効率的な証明法を提供できるため,定理自動証明,関数型あるいは論理型言 語,代数的仕様記述,記号処理など,計算機科学のさまざまな分野で広くもち いられています.
項書き換えシステムは方向付けられた等式(書き換え規則)の集合として 定義されます.ところで,等式そのものにはもともと計算という意味はありま せん.たとえば,等式 1+2 = 3 は右辺と左辺が等価であるという論理的な意 味をもつだけです.したがって,論理の世界では,1+2 から 3 を得るだけ ではなく,逆に 3 から 1+2 を得ることも可能です.

一方,この等式を計算という立場でながめてみると, 1+2 の計算結果として 3 が得られるのであり,3 の計算結果として 1+2 が 得られることはありません.このように,等式 1+2 = 3 を複雑な式から単純 な式への非可逆な書き換え規則 1+2 → 3 とみなすと,等式で表された平面的 な論理の世界を高低差のある計算の世界に自然な形で結び付けることが可能と なります.
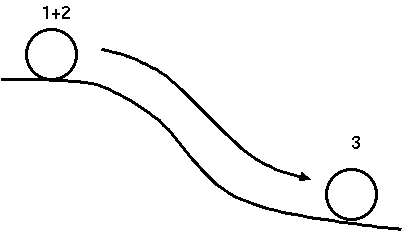
項書き換えシステムの計算は,これらの書き換え規則を繰り返し適用する ことによって与えられた項がもっとも単純な形(正規形)に到達するまでリダ クションすることで実現されます.たとえば,項 (5 * 4) + (3 * 2) にリダ クションを繰り返すと最後には正規形 26 が求まります.
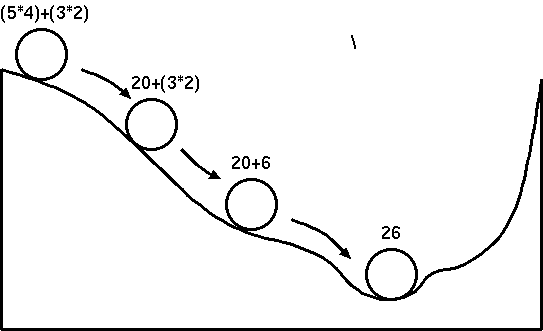
項書き換えシステムをもちいることに より,等式にもとづいて記述された関数型プログラムや代数的仕様記述に,自 然な形でリダクションにもとづく操作的意味を与えることができます.また,自 動証明における等式推論をリダクションで実行することにより,証明を効率的 な計算に置き換えることも可能となります.とくに,完備な項書き換えシステムを もちいると,バックトラッキングが不要となるため,きわめて高速な等式自動 証明システムを実現することができます.ここでは,項書き換えシステムをもち いた等式証明で中心的な役割をはたす完備化手続き(Completion)に焦点をしぼ り,自動証明において項書き換えシステムがどのように応用されているかを解 説します.
自然数上の加算を例にとり項書き換えシステムの考え方を説明します.まず,自 然数上の加算 + を等式システムで表してみましょう.話を簡単にするために, 以下では自然数 0, 1, 2,... を 0,s(0),s(s(0)),... で表現することにします.すると自然数 x の次の数は s(x) とな るから加算 + は以下の等式システム E で形式化できます.
| x+0 = x |
| x+s(y) = s(x+y) |
ここでシステムを記述している等式 s = t を左辺から右辺への非可逆な書き換 え規則 s → t とみなしたものが項書き換えシステム (term rewriting system) です.等式システム E からは以下の項書き換えシ ステム R が得られます.
| x+0 → x |
| x+s(y) → s(x+y) |
このとき 1+2 = 3 の計算は R の書き換え規則を適用して以下のリダクショ ン(項の書き換え)を行うことによって得られます.
ここで 項 s(s(s(0))) はこれ以上リダクションすることができません.こ のような項を正規形 (normal form) とよびます.正規形はリダクションによ る計算の答えとみなせます.項 s から 項t (t は正規形である必要はありま せん)に0回以上のリダクションで到達できるとき s →* t と書 きます.したがって,上記のリダクションは s(0)+s(s(0)) →* s(s(s(0))) と表せます.
加算 + と乗算 * をあらわす項書き換えシステム R' を以下に示します. 加算と乗算が書き換え規則のみで完全に実現されていることに注意してください. 実際,すべての計算可能な関数は有限個の書き換え規則で完全に表せるこ とが知られており,項書き換えシステムは計算モデルとして十分な計算能力を もっています.
| x+0 → x |
| x+s(y) → s(x+y) |
| x*0 → 0 |
| x*s(y) → (x*y)+x |
ここでは,項書き換えシステムの基本的な性質である合流性(チャーチ・ロッ サ性),停止性,完備性について簡単に紹介します.
項書き換えシステムでは,与えられた項からのリダクションの道筋は一通 りとは限りません.項に適用可能な書き換え規則も,その規則を適用できる部 分も一般には一意に決まらないからです.したがって,書き換え規則の適用順 序の違いによって,何通りものリダクションの道筋が可能となります.たとえ ば,さきほどの R' における項 (s(0)*0)+(s(0)+0) のリダクションは次のよ うになります.
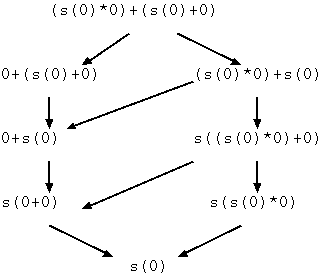
この例では途中のリダクションの道筋とは関係なく,すべてのリダクションは 唯一の正規形 s(0) に合流しています.一般の項書き換えシステムでは,この ような合流性は必ずしも保証されていません.もし,上図のようにリダクション の合流性が常に保証されているならば,項書き換えシステムは合流性(チャー チ・ロッサ性)をみたすといいます.正確に述べると,項書き換えシステムが合流 性をみたすとは,任意の項 t をリダクションして項 s,r を得たなら ば,必ず s と r から合流できる項 p が下図のように存在することです.
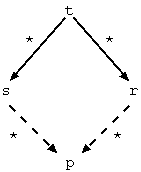
項書き換えシステムのリダクションが必ず停止するならば,項書き換えシステ ムは停止性 (強正規性) をみたすといいます.項書き換えシステムが合流性と停止 性をみたすなら,完備 (complete) であるといいます.等式システム E から得 られた完備な項書き換えシステム R は次の重要な性質をもっています.
性質1は,s の正規形 s↓ が必ず存在し,どのようなリダクショ ンで正規形を求めても s↓ に一致することを保証しています.つま り,非決定的な計算において,どのような計算で答えを求めても常に正しい答 えが得られることを意味しています.
性質2は,等式システムによる s = t の証明がリダクションによる効率的 な計算でおこなえることを意味しています.すなわち,通常の証明が試行錯誤 を繰り返しながら進むのに対して,合流性をみたす項書き換えシステムによる 証明では s と t のリダクションのみを考えれば十分であり,試行錯誤はまっ たく不要になります.このことを少し詳しく説明しましょう.
項書き換えシステムR が完備であるなら s = t の証明は次のようにおこな えばよいことがわかります.まず, s と t にリダクションをおこない 正規 形 s↓,t↓ を求めます.ここで,R の停止性からそれぞれのリダクションは 必ず止まり,性質1から正規形は一意に求まることに注意してください.この とき,二つの項が同じ形をしていることを ≡ で表すと,s↓ ≡ t↓ ならば s = t は成立し,s↓ ≡ t↓ でないならば s = t は成立しないことがわかり ます.つまり,完備な項書き換えシステムが与えられると,等式 s = t の証 明問題は決定可能となります.
このように,与えられた等式システム E を項書き換えシステム R とみな したときに,R が完備になっているならば等式証明問題は効率的に解くことが できます.しかし,一般には等式を左から右への書き換え規則とみなすだけで は,完備な項書き換えシステムは得られません.そこで,等式システム E を 論理的に等価なシステムに変形することにより,完備な書き換えシステムを構 成する完備化手続きが広く利用されています.完備化手続きの基本的なアイデ アを以下ではパズルをもちいて説明しましょう.

酒のグラス S,ウィスキーのグラス W,ビールのグラス B が以下のように一 列に並んでいます.
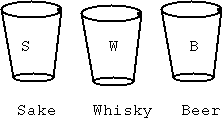
このとき,次のグラスの置き換えシステム G によって,グラス列を自由に置 き換えることを考えます.
| W = SW |
| WB = S |
置き換え規則 W = SW は W を2個のグラスの並び SW に置き換えてもよい し,その逆に SW を1個のグラス W に置き換えてもよいことを示しています. たとえば,最初に示したグラス列 SWB は以下のようにグラス列 WBWB に置き 換えることができます.
このときグラス列 SWB と WBWB はグラス置き換えシステム G によってつ なぐことができるといいます.それでは以下のグラス列はうまくつながるでしょ うか.
問題 1. SSWB = ・・・ = WBWB ?
問題 2. SSSW = ・・・ = WBWB ?
この問題の難しさは,二つのグラス列をつなぐことが不可能な場合に,ど うやってそれを示すかという点にあります.もし,グラス列をつなぐことが可 能ならば,試行錯誤を繰り返していくことで答えをいつか発見することができ るでしょう.しかし,不可能な場合には,すべての置き換えがグラス列をつな ぐことに失敗することを示す必要があります.置き換えの可能性は無限にあり ますから,これらをすべて検査していては永久に答えは得られません.そこで, 完備な書き換えシステムをもちいてこのパズルを解く方法を考えてみます.
グラス置き換え規則を方向付けてやることにより,置き換えシステム G か ら停止性をもつ書き換えシステム R を以下のように構成してみましょう.
| SW → W |
| WB → S |
ここで,書き換えシステム R が完備となるならば,二つのグラス列がつな がるか否かという問題は,グラス列の正規形が一致するか否かという問題に還 元できるので完全に解くことが可能です.さて,書き換えシス テム R のリダクションは書き換えによってグラス列を短くするので,R が停 止性をみたすことは明らかです.しかし,グラス列 SWB は以下のように二つの正規形 S と SS に発散してしまうので,R は合流 性をもちません.つまり,書き換えシステム R は完備ではないことになります.

それでは,R がグラス列 SWB に対して合流性をみたさない原因を考えてみ ましょう.上記のリダクションでは二つの書き換え規則 SW → W と WB→ S の適用が SWB で可能となっており,グラス W でそれぞれの書き換え規則の左 辺は重なっています.したがって,一方の書き換え規則の適用は,そこに重なっ ている他方の書き換え規則の適用を不可能にしてしまい,その結果としてリダ クションの合流性が破壊されてしまいます.この例では,二つの規則の左辺の 重なりSWB にそれぞれの規則を適用して WB と SS が得られ,さらに WB と SS が異なる正規形をもつことから合流性が壊されます.
以上のように,二つの書き換え規則に重なりがあると合流性は無条件には 成立しません.二つの規則の左辺の重なり SWB に対して,それぞれの規則を 一回づつ適用して得られる値の対 <WB, SS> を危険対とよびます.危険対の 要素をそれぞれリダクションして正規形を求めたとき,両者が一致するなら危 険対は収束する,一致しないならば発散するといいます.つまり,R が合流し ないのは危険対 <WB, SS> が発散しているからです.項書き換えシステムの 書き換え規則が有限個ならば,書き換え規則の重なりも有限の可能性しかあり ませんから,危険対も有限個しかないことに注意して下さい.このとき,以下 の合流条件が知られています.
Knuth-Bendix の合流条件. 停止性をみたす項書き換えシステム R が合流性(つまり完備性)をもつための必要十分条件は,R のすべての 危険対が収束することである.
したがって,書き換えシステム R を完備にするためには,論理的に等価な
変形をおこなって,発散する危険対をうまく消してやればよいことがわかりま
す.発散する危険対
ここで注意してほしいのは,新しく付け加えられた規則 SS → S は,もと
の置き換え規則を組み合わせることによって以下のように G でシミュレーショ
ンできることです.
したがって,グラス置き換えパズルの本質は,付け加えられた規則によって変更さ
れていません.つまり,書き換えシステム R のかわりに書き換えシステム R'の
もとでパズルを解いてもよいことがわかります.ここで,新しく得られた R' の書き
換え規則の重なりをチェックすると,すべての危険対が収束することを容易に
示せます.したがって,R' は完備な書き換えシステムとなっています.
先ほどのグラス置き換え問題1と2は,完備な R' によるリダクションで
簡単に解くことができます.問題1では,SSWB↓ ≡ S ≡ WBWB↓ となり正規
形が一致するので,グラス列は置き換え規則 G でつなぐことができます.一
方,問題2では,SSSW↓ ≡ W および WBWB↓ ≡ S となり正規形は異なるの
で,グラス列を G でつなぐことができません.
グラス置き換えパズルの例では,書き換えシステム R の発散する危険対か
ら作られた書き換え規則を付け加えるだけで,完備な書き換えシステム R'
を得ることができました.しかし,一般には新しい書き換え規則を付け加えること
によって,発散する危険対が新たに生ずる可能性もあります.したがって,このよ
うな場合には発散する危険対が完全になくなるまで,次々と新しい書き換え規
則を付け加えていく必要があります.また,書き換え規則の両辺が他の規則によっ
てリダクションできるのならば,両辺をリダクションして正規形にした方がシ
ステムは単純になり,発散する危険対の生成も押えられます.このような点まで
考慮した Kunuth-Bendix の完備化手続きを以下に示します.
ここで > は停止性を保証するための適当な順序であり,R のすべての書
き換え規則 s → t が s > t をみたすなら R は停止性をみた
すものとします.手続きは最初 R を空集合とし,適当な等式の集合 E を与
えて実行を開始します.そして, E が空集合になれば完備化は成功し,完備な
項書き換えシステム R が得られます.なお,この手続きはループを永久に
回り続けて停止しない場合があることに注意してください.
完備化手続きをもちいて群を完備化した例を示します.群の公理で
ある左単位元の存在,左逆元の存在,結合律は以下の等式システム E で
表されます。
ここで,完備化手続きを E に適用すると,最終的には以下の10個
の規則からなる完備な項書き換えシステム R を得ることができます.
このとき,E のもとで等式 s = t が成立するか否かという語の問題は, R
によって完全に解くことができます.なぜなら,E のもとで等式 s = t が成
立することと,R のもとで s↓ と t↓ が一致することは等価となるからでで
す.
ペトリネットは1962年に Petori によって提案されたイベント駆動型
システムのモデルで,並行プロセスの記述などに広く利用されています.ここ
では,ペトリネットを変形した両方向ペトリネットの到達可能性問題が完備化
によって解けることを示しましょう.まず,両方向ペトリネットの発火動作を
以下の図で説明します.
トランジション A の左に結合しているプレース a と b に,A とプレース
を結ぶアークの個数以上のトークン(小石)が存在すれば,A は左から右へ発火
可能です.ここで A が左から右へ発火すると,A の左に結合しているプレー
ス a と b から,A とプレースを結ぶアークの個数だけトークンを取り除き,
A の右に結合している各プレース c と d に,A とプレースを結ぶアークの個
数だけトークンを増加させます.右から左への発火も同様に定めることができ
ます.もし,A を左から右へ発火させた直後に,今度は A を右から左に逆向
きに発火させると,トークンは元にもどります.通常のペトリネットではアー
クが方向付けられているので発火も片方向だけですが,両方向ペトリネットで
はアークが両方向に利用できるので,両方向の発火が可能となることに注意し
てください.
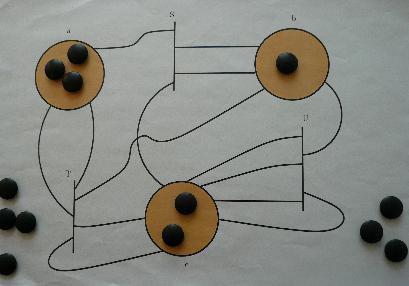
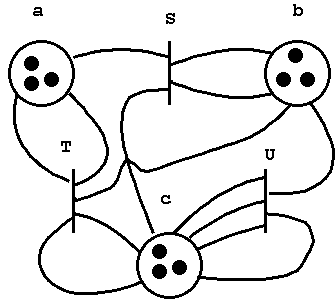
両方向ペトリネットのプレース a に3個のトークンが存在する状態を aaa
で表すことにします.したがって,上図の両方向ペトリネットの状態は
aaabbbccc となります.(もちろん,bbbcccaaa や abcabcabc と表すこともで
きます.) このとき,トランジション S,T,U を適当な順序で右から左ある
いは左から右へ発火させることにより状態 abc へ到達可能か否かという到達
可能性問題を考えましょう.
まず,上図の両方向ペトリネットのトークンの変化を等式システム E で表
します.ここで,等式 ac = bb はトランジション S が右から左あるいは左か
ら右へ発火したときの各プレース上のトークンの個数の変化を表現しています.
このとき,完備化手続きを E に適用すると以下の完備な項書き換え
システム R が得られます.
したがって,両方向ペトリネットの状態 aaabbbccc から状態 abc への到
達可能性は,R のもとで aaabbbccc↓と abc↓ が一致するか否かを調べるこ
とで判定できます.実際,aaabbbccc↓ ≡ cccccc ≡ abc↓ となるので到達
可能であることがわかります.
完備化手続きによって組ひも問題が簡単に解けることを示します.完備化
にもとづく等式証明は,組ひも問題のような3次元トポロジーの問題に対して
も極めて有効です.
組ひも群 (The Braid Group)は,
まっすぐなひもからなる組ひもを単位元 e とし,
構成要素(1) σ[i] と (2)
σ[i]-1 ( i = 1, ... , n ) の積構造でつ
くられる群であり,以下の組ひも関係式をみたします.
σ[i]σ[i+1]σ[i] = σ[i+1]σ[i]σ[i+1] ( 0 < i < n )
σ[i]σ[j] =σ[j]σ[i] ( | i - j | > 1 )
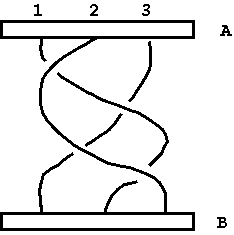
今,以下のように3本の組ひもの片方を A に固定し,もう一方の端に木片
B を取り付けます.ここで,木片 B を裏返さずにひもの間をくぐらせる基本操
作のみで,まっすぐな組ひも(つまり単位元 e)にもどせるか否かを決定する問
題を,Dirac の組ひも問題とよびます.
項書き換えシステムの完備化をもちいてDirac の組ひも問題を解くためには,
まず 8 通りの基本操作と組ひも群の公理を等式システム E で以下のように
表します.
このとき,E に対して完備化手続きを適用すると19個の書き換え規則か
らなる完備な項書き換えシステム R が得られ,Dirac の組ひも問題は決
定可能となることがわかります.
完備化手続きにおいて,与えられた等式システム E の等式 s = t (あるい
は t = s)から書き換え規則 s → t を得るためには,停止性を
保証するための適当な順序 > のもとで s > t をみたす必要があります.もし,
どの等式も順序 > のもとで向き付けができないなら完備化手続きは失敗しま
す.
しかし,等式そのものは向き付けが不可能であっても,実際の書き換えの適用
においては向き付けができる場合があります.
例えば,関数 f に関する交換律 f(x, y) = f(y, x) を考えましょう.
この等式に
対して停止性を保証できる向き付けは存在しません.しかし,2 > 1 のとき,
値 1 と 2 を変数 x と y へ代入することで得られた等式 f(2, 1) =
f(1, 2) は,f の引数の辞書式順序をもちいることにより f(2, 1)
→ f(1, 2) と向き付けることが可能となります.
つまり,f(x, y) = f(y, x) を両方向に使える可能性のある書き換え規則とみ
なし,適当な代入で停止性が保証される向き付けが得られた場合にのみ,この等
式を向き付けられた書き換え規則として適用してリダクションを行うことにし
ます.したがって,4 > 3 > 2 > 1 ならば f(f(4, 3), f(2, 1))
→* f(f(1, 2), f(3, 4)) なるリダクションが
得られることになります.
このように,向き付けできない等式も両方向に使える書き換え規則とみなして
完備化を行うと,等式の向き付けができなくて完備化が失敗することはなくな
ります.この方法で拡張された完備化は失敗無し完備化 (unfailing
completion)あるいは無向完備化とよばれます.
失敗無し完備化手続きでは失敗して手続きが停止することはありません.
しかし,手続きが永久に走りつづける可能性は依然残っています.この場合に
も,失敗無し完備化が生成し続ける書き換え規則をもちいて,s と t の合流
性判定を完備化と並行して行うと,等式 s = t に関して完全な証明システム
が得られます.このため,失敗無し完備化手続きは,完全な等式証明法として
自動証明システムに広くもちいられています.
項書き換えシステムの重要な性質である完備性と,その自動証明への応用であ
る完備化手続きについて説明しました.実際の自動証明システムでは,完備化
以外にもさまざまな等式証明の技術が使われています.例えば,結合律や交換
律のような特別な等式規則の効率的処理,スコ−レム化による反駁証明,書き
換えシステムの停止性自動判定,潜在帰納法や書き換え帰納法をもちいた帰納
的定理の自動証明法などは広く使われている重要な証明技術です.さらに,多
くのシステムでは等式論理のみではなく,述語論理や高階論理を取り扱うこと
も可能です.
ここで紹介した内容は,項書き換えシステムの理論と応用のごく一部に過
ぎません.項書き換えシステムについてさらに知りたい方には,以下の教科書
をお薦めします.初心者向けとして丁寧に書かれており内容も良くまとまって
います.
F. Baader and T. Nipkow, なお,本ページの内容は以下の解説を修正・加筆したものです.参考文献
等に関心のある方はご覧ください.
最後になりましたが,ここで紹介したさまざまな完備化の例は,私たちの
研究室のセミナーや実験の課題として長年取り上げてきたものです.これらの
実験に協力いただいた研究室のスタッフならびに学生のみなさんに心より感謝
いたします.

SW → W
WB → S
SS → S
完備化手続き
R は書き換え規則の有限集合,E は等式の有限集合,> は停
止性を保証する項上の順序とする.また,危険対 <p, q> を
E の中では等式 p = q で表す.R の初期値は空集合とする.
E が空でないならば以下を繰り返せ. E が空になれば完備化
は成功.
(1) E から s > t をみたす 等式 s = t (あるいは t = s)
をひとつ取り除く.もし,そのような等式がないなら完備化は失敗.
(2) 書き換え規則 s → t でリダクションできる R の
書き換え規則をすべて E に移す.
(3) s → t と R
によって生じたすべての危険対を E に付け加える.
(4) s → t を R に付け加える.
(5) R をもちいて R のすべての
書き換え規則の右辺を正規形にする.
(6) R をもちいて E の等式の両辺をすべて正規形にする.両辺が
一致した等式は E から取り除く.
群の完備化
1*x = x
I(x)*x = 1
(x*y)*z = x*(y*z)
I(1) → 1
1*x → x
x*1 → x
I(I(x)) → x
I(x)*x → 1
x*I(x) → 1
I(x*y) → I(y)*I(x)
(x*y)*z → x*(y*z)
I(x)*(x*y) → y
x*(I(x)*y) → y
両方向ペトリネットの完備化

ac = bb (S)
ac = abc (T)
ccc = bc (U)
ab = ba
bc = cb
ac = ca
ccccccc → ccccc
bb → cccccc
cb → ccc
bc → ccc
ab → ba
ca → cccccc
ac → cccccc
組ひも問題の完備化


((σ[1] σ[2] ) σ[2]) σ[1] = e
((σ[1]-1 σ[2]-1) σ[2]-1) σ[1]-1 = e
((σ[2] σ[1]) σ[1]) σ[2] = e
((σ[2]-1 σ[1]-1) σ[1]-1) σ[2]-1 = e
((σ[1] σ[1]) σ[2] )σ[2] = e
((σ[1]-1 σ[1]-1) σ[2]-1) σ[2]-1 = e
((σ[2] σ[2]) σ[1]) σ[1] = e
((σ[2]-1 σ[2]-1) σ[1]-1) σ[1]-1 = e
σ[1]-1 σ[1] = e
σ[1] σ[1]-1 = e
σ[2]-1 σ[2] = e
σ[2] σ[2]-1 = e
(σ[1] σ[2]) σ[1] =
(σ[2] σ[1]) σ[2]
e x = x
x e = x
(x y) z = x (y z)
σ[2] σ[1] →
σ[1] (σ[1] (σ[2] σ[1]-1))
σ[2] σ[2] → σ[1] σ[1]
σ[2] (σ[1] (σ[1] x)) →
σ[1] (σ[1] ( σ[2] x))
σ[1] (σ[1] (σ[1] (σ[1] x))) → x
σ[1]-1 x → σ[1] (σ[1] (σ[1] x))
σ[2]-1 x → σ[1] (σ[1] (σ[2] x))
σ[2] (σ[1] σ[2]) →
σ[1] (σ[1] (σ[1] (σ[2] σ[1]-1)))
σ[2] (σ[1] σ[1]) → σ[2]-1
σ[1] (σ[1] σ[2]) → σ[2]-1
σ[1] (σ[1] σ[2]-1) → σ[2]
σ[1] (σ[1] σ[1]) → σ[1]-1
σ[2] (σ[1] σ[2]-1) →
σ[1] (σ[2] σ[1]-1)
σ[2] (σ[2] x) → σ[1] (σ[1] x)
σ[2] σ[2]-1 → e
σ[1] σ[1]-1 → e
σ[2] (σ[1] (σ[2] x)) →
σ[1] (σ[2] (σ[1] x))
e x → x
x e → x
(x y) z → x (y z)
失敗無し完備化
おわりに
Term Rewriting and All That,
Cambridge University Press, 1998.
完備化による等式証明,
人工知能学会誌, Vol.16, No.5, pp.668-674, 2001.
[PDFファイル]
項書き換えシステム入門,
信学技報, SS98-15, pp.31-38, 1998.
[PDFファイル]
[外山研究室]
[電気通信研究所]
[東北大学]
ご意見お問い合わせは
webmaster まで.
まで.